![[Up]](../images/up.gif) 1 Einleitung
1 EinleitungInhalt
1 Einleitung
2 Das Modell
2.1 Kosten, Erlöse und Gewinne
2.2 Die Produktionsentscheidung
3 Die Verhandlungen
3.1 Ablauf der Verhandlungen
3.2 Verhandlungslösungen
3.3 Plausibilität der Lösungen
4 Konsequenzen der Verhandlungslösungen
4.1 Verhandlungsstärke
4.2 Symmetrie und Effizienz
4.3 Unternehmensorganisation
Anhang
Herleitung von wk und wA
Abkürzungsverzeichnis
Symbolverzeichnis
Literaturverzeichnis
![[Up]](../images/up.gif) 1 Einleitung
1 EinleitungZunächst soll die Produktionsentscheidung dargestellt werden, dann folgt eine Darstellung der Lohnverhandlungen. Schließlich soll in Kapitel 4 betrachtet werden, welche Auswirkungen sich daraus für AN und KE hinsichtlich der Beteiligung am Unternehmensgewinn einerseits und der Unternehmensführung andererseits ergeben. Außerdem wird betrachtet, wie sich die Verhandlungslösungen auf die Effizienz der Produktionsentscheidung auswirken.
![[Up]](../images/up.gif) 2 Das Modell
2 Das ModellKapital und Arbeit können nun aber immer nur von verschiedenen Parteien bereitgestellt werden (Keine vertikale Integration). Als Grund dafür könnte angeführt werden, daß Gemeinschaftsbesitz der AN zu schwer zu verwalten ist oder daß AN nicht genug Kapital haben, um erforderliche Investitionen zu tätigen. Auf seiten der KE mag der Bedarf an Arbeit im Produktionsprozeß das Angebot, das die KE selbst bereitstellen könnten, bei weitem übertreffen. Dies scheint empirisch gerechtfertigt, zumindest in großen Firmen sind Arbeit und Kapital meist getrennt.
Aus diesem Grund muß der eine Faktor vom anderen angeheuert werden. Es soll zunächst davon ausgegangen werden, daß die KE die AN anheuern. Zwischen beiden Parteien kommt es zu Verhandlungen über die Entlohnung der AN. Alle Zusammenhänge gelten aber auch, wenn AN Kapital anheuern. Es kehren sich dann lediglich die Rollen um. Die Verhandlungen verlaufen nach den Regeln des Rubinsteinspiels, worauf in Kapitel 3 ausführlich eingegangen wird.
Es wird nur über den Lohn verhandelt. Dow schließt Ausgleichszahlungen zwischen den Parteien aus.1 Es kann nicht ein bestimmter Lohn zum Zwecke der Gewinnmaximierung vereinbart werden und dann der Gewinn durch Ausgleichszahlungen zwischen KE und AN aufgeteilt werden.
Der Lohn wird unabhängig von der Ausbringungsmenge festgelegt. D.h. Akkordlöhne oder ähnliches sind nicht möglich. Dies ist z.B. im Dienstleistungsbereich durchaus realistisch, weil der Einfluß des einzelnen AN auf die 'Produktionsmenge' nicht exakt meßbar ist.2 Ebenfalls kann die Ausbringungsmenge nicht verhandelt werden, sie wird nach Abschluß der Lohnverhandlungen einseitig von den KE festgelegt. Allerdings gibt es eine maximale Ausbringungsmenge, die die AN zu gegebenen Lohn bereit zu produzieren sind (siehe 2.2).
![[Up]](../images/up.gif) 2.1 Kosten, Erlöse und Gewinne
2.1 Kosten, Erlöse und GewinneDie Unternehmung operiert als Mengenanpasser in einem Markt mit vollkommener Konkurrenz und freiem Eintritt. Die Erlöse ergeben sich aus der produzierten Menge x und dem Marktpreis p, wobei der Marktpreis als exogene Größe eingeht und der Absatz beliebiger Mengen als gesichert gelten soll.
(1) Erlösfunktion: E(x) = px.
Aus Kosten und Erlösen ergibt sich dann die Gewinnfunktion.
(2) Gewinnfunktion: G(x) = px - kk(x) - kA(x).
Abbildung 2.1: Kosten, Erlöse und Gewinn
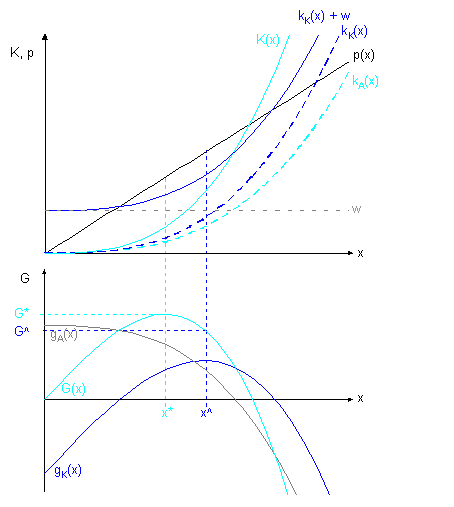
Zeichnung: IML '97
Aus Abbildung 2.1 ergibt sich die für die Unternehmung optimale Produktionsmenge x*. Der Gewinn entspricht dem Abstand zwischen den Graphen der Gesamtkostenfunktion K(x) = kk(x) + kA(x) und der Erlösfunktion E(x). Mathematisch erhält man die gewinnmaximale Menge x* durch E'(x) = K'(x).
![[Up]](../images/up.gif) 2.2 Die Produktionsentscheidung
2.2 Die Produktionsentscheidung(3) Gewinnfunktion der KE: gk(x) = px - kk(x) - w.
Die KE können die Produktionsmenge nach Abschluß der Lohnverhandlungen frei wählen. Ihre einzige Beschränkung ist, daß die AN mindestens einen Gewinnanteil von Null aus der Mitarbeit beziehen müssen. Der Gewinnanteil der AN berechnet sich aus dem gezahlten Lohn w, von dem der Arbeitsaufwand kA(x) abgezogen werden muß.
(4) Gewinnfunktion der AN: gA(x) = w - kA(x).
Es sind daher prinzipiell zwei Fälle bei der Produktionsentscheidung zu berücksichtigen:
(I) Unbeschränkte Produktionsmenge:
Die Menge x^, die den Gewinnanteil der KE gK(x) maximiert, kann produziert werden. Der gegebene Lohn w übersteigt das Arbeitsleid der AN, und diese erhalten einen Gewinnanteil von Null oder mehr.
(5) x(w) = x^ wenn w kA(x^).
Es fließen hier die Kosten der AN nur indirekt über den Lohn ein. Dies ist auch der Grund dafür, daß mit x^ eine suboptimale Menge gewählt wird. Der maximale Unternehmensüberschuß wird bei der niedrigeren Menge x* erzielt . In diesem Sinne wird überproduziert.3
(II) Produktionsmenge mit Arbeitsangebotsbeschränkung
Die Menge x^ kann nicht hergestellt werden, wenn der Lohn das Arbeitsleid der AN nicht ausgleicht (w < kA(x^)). Die AN sind dann nicht bereit, x^ zu produzieren. In diesem Fall werden die KE die maximale Menge, die die AN bei gegebenen Lohn bereit zu produzieren sind, wählen. Dies ist aus Abbildung 2.1 ersichtlich: Von x^ nach x* nimmt der Gewinnanteil der KE, repräsentiert durch die Differenz von E(x) und kK(x) +w stetig ab.4 Ist x^ nicht möglich, ist die Menge, die x^ am nächsten kommt, optimal für die KE. In diesem Falle berücksichtigen die KE die Kosten der AN in vollem Maße, weil w = kA(x).
(6) x(w) = x [kA(w)] wenn w < kA(x^).
Obwohl es in den im folgendem zu besprechenden Lohnverhandlungen um die Verteilung des Gewinns geht, wird nur der Lohn konkret verhandelt. Dieser wirkt sich allerdings indirekt auf die Höhe des zu verteilenden Gewinns sowie die Verteilung des selbigen zwischen den Parteien aus. Um diesem Rechnung zu tragen, muß die Lohnhöhe in Zusammenhang mit der Gewinnhöhe G(w) sowie der Gewinnanteile von AN und KE, gA(w) und gk(w), gebracht werden. Es muß hier wiederum zwischen den Fällen mit beschränkter und unbeschränkter Produktionsmenge unterschieden werden.
(I) Unbeschränkte Produktionsmenge (w > w^):
w^ sei definiert als der Lohn, bei dem die AN gerade bereit sind, die von den KE bevorzugte Menge x^ zu produzieren. w^ ist daher genau gleich des bei dieser Menge entstehenden Arbeitsaufwands kA(x^). Aus Gleichung (4) ergibt sich somit, daß ihr Gewinnanteil null ist. Erhalten sie nun aber den Lohn w, so ist die Differenz zu w^ ihr Gewinnanteil.
(7) gA(w) = w - w^.
Als Überschußberechtigter erhalten die KE selbstverständlich das, was vom Gewinn nach Lohnzahlung noch übrig ist. Dies ist der Gesamtgewinn abzüglich des an die AN fallenden Anteils.
(8) gk(w) = G^ - (w- w^).
Hierbei sei G^ = G(x^) der Gewinn, der bei der von KE bevorzugten Menge x^ anfällt. Bezeichnet w° den Lohn, bei dem die AN den gesamten Gewinn vereinnahmen und w^ den Lohn, bei dem die AN nichts vom Gewinn bekommen, so muß gelten G^ = w° - w^, so daß schließlich gilt:
(10) gk(w) = w° - w^ - (w- w^) = w° -w.
(II) Beschränkte Produktionsmenge (w < w^):
Wie oben bereits erörtert, wählen die KE in diesem Fall (II) die maximale Menge, die die AN bei gegeben Lohn bereit zu produzieren sind. In diesem Fall sind w^ und w identisch, und der Gewinnanteil der AN muß null sein.
(11) gA(w) = 0.
Ist der Gewinnanteil der AN null, fällt der gesamte zu verteilende Gewinn, an die KE. Der Gewinn wiederum ist abhängig von der Menge, die bei gegebenem Lohn von den AN maximal produziert wird. Anders als im Fall (I) variiert der zu verteilende Gewinn also mit der Lohnhöhe.
(12) gk(w) = G[(x(w)].
Abbildung 2.2: Gewinn und Lohnzahlung
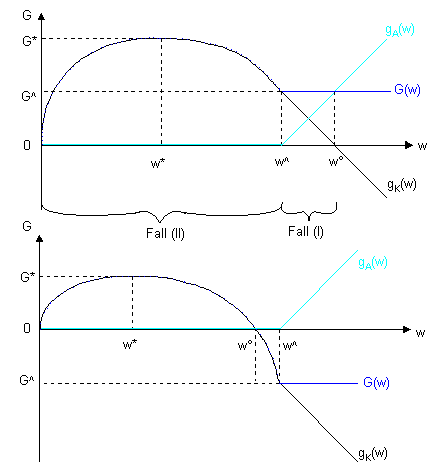
Quelle: nach Dow (1993), S. 124
Abbildung 2.2 zeigt die jeweiligen Gewinnfunktionen G(w), gk(w) und gA(w). Der linke Teil in jeder Grafik repräsentiert Fall (II). Der Gewinnanteil der AN gA(w) ist null, der Gesamtgewinn G(w) ist variabel mit einem Maximum bei w*. Bei höheren Löhnen steigt die Ausbringung weiter, während der Überschuß sinkt, bis beim Lohn w^ die von KE bevorzugte Menge x^ erreicht wird. Der Gesamtgewinn bleibt danach konstant, der Lohn entscheidet nur noch über die Verteilung des Nutzens. Je höher der Lohn wird, ein desto größerer Teil fällt an die AN. Beim Lohn von w° erhalten die AN den gesamten Gewinn.
Die obere und untere Grafik unterscheiden sich in Hinblick auf G^. Im unteren Fall ist G^ < 0 und für die AN nur ein positiver Gewinnanteil möglich, wenn der der KE negativ wird. Diesem kommt bei der Diskussion der Verhandlungslösungen in den nächsten Kapiteln besondere Bedeutung zu.
![[Up]](../images/up.gif) 3 Die Verhandlungen
3 Die Verhandlungen![[Up]](../images/up.gif) 3.1 Ablauf der Verhandlungen
3.1 Ablauf der VerhandlungenEs werden solange wechselseitig Vorschläge gemacht, bis sich AN und KE auf einen Lohn einigen oder die Verhandlungen abbrechen. Im ersten Fall wird die Zahlung des Lohns verbindlich, und es kommt zur Produktion der Menge, die die KE gemäß dem im Kapitel 2.2 ausgeführtem wählen. Im letzteren Fall kommt es nicht zur Produktion, und beide Parteien erzielen weder einen Nutzen noch haben sie laufende Kosten. Aus letzterem ergibt sich auch, daß keine der Parteien in eine Beteiligung an der Produktion einwilligen wird, wenn sie daraus einen negativen Nutzen ziehen würde.
Da das Nash-Gleichgewicht beim Rubinsteinspiel (RS) zu unendlich vielen Lösungen führt, wird für die Lösung das Konzept der Teilspielperfektheit herangezogen. Teilspielperfekt ist eine Strategiekombination zweier Spieler nur, wenn es für keinen der Spieler optimal ist, bei irgendeinem Teilspiel aus dem Spielbaum von seiner Strategie abzuweichen. Dadurch wird ausgeschlossen, daß es zu einer Lösung kommt, die eine unglaubwürdige Drohung eines Spielers beinhaltet. Eine unglaubwürdige Drohung wäre im RS, wenn ein Spieler droht, ein Angebot abzulehnen, obwohl er sich durch sein eigenes Angebot in der Folgeperiode schlechter stellen würde.5 Darüber hinaus soll angenommen werden, daß beide Spieler, AN und KE, stationäre Strategien spielen. Das heißt die Strategie ist unabhängig von Vorkommnissen in Vorperioden. Außerdem soll angenommen werden, daß ein Spieler, wenn er zwischen dem Ergebnis, das er in Periode t und dem, das er in Periode t+1 erzielen kann, indifferent ist, bereits den Vorschlag aus Periode t annimmt.
![[Up]](../images/up.gif) 3.2 Verhandlungslösungen
3.2 VerhandlungslösungenTabelle 3.1:6
| Periode | Vorschlags-
recht hat |
Angebot und Annahme von Vorschlägen | |
| KE | AN | ||
| t0 | KE | bieten wK
-> nK (wK, t0) = w° - wK
|
akzeptieren
nA dA(wA - w^) |
| t1 | AN | akzeptieren
nK dK( w° - wK) |
bieten wA
-> nA (wA, t1) =dA(wA
- w^)
|
| t2 | KE | bieten wK
-> nK (wK, t2) = dK2(w°
- wK)
|
akzeptieren
nA dA(wA - w^) |
Wenn die KE den ersten Vorschlag machen, bieten sie per Definition wK, welches für die AN zu einem Nutzen von nA(wK, t0) führt (Siehe Tabelle 3.1). Ihr Ziel ist es, die AN indifferent zwischen Annahme des Vorschlags und Formulierung eines eigenen Vorschlags in der Folgeperiode zu machen. Sie wollen die AN deshalb indifferent machen, weil, wenn sie weniger böten, die AN ablehnen würden und kostbare Zeit verloren ginge. Sie bieten nicht mehr, weil sie sich selbst sonst unnötig schlechter stellen würden. Die AN sind dann indifferent zwischen Annahme und Ablehnung, wenn wK ihnen soviel bietet, wie der Vorschlag, den sie in t1 machen könnten. Per Definition bieten die AN in t1 wL, welches einen Nutzen von nA(wA, t1) für sie selbst und nK(wA, t1) für KE bedeutet. Auch sie werden versuchen, die KE indifferent zwischen Annahme und Ablehnung des Angebots zu machen. Die KE wiederum sind indifferent, wenn wL ihnen soviel bietet, wie ihr eigener Vorschlag in t2. Wegen angenommener Stationarität der Strategien, bieten die KE in t2 wieder wK, was ihnen dann einen Nutzen nK(wK, t2) beschert.
Somit lassen sich zwei Gleichungen zur Lösung der beiden Unbekannten wK und wL finden. KEs Vorschlag muß Gleichung (13) erfüllen, ANs Vorschlag Gleichung (14).
(13) nA(wK, t0) = nA(wA,
t1),
(14) nK(wA, t1) = nK(wK,t2).
Setzt man die Werte aus Tabelle 3.1 ein und löst das Gleichungssystem (siehe Anhang), so erhält man
(15) ![]() ,
,
(16) ![]() .
.
wobei wK den Lohn darstellt, auf den sich beide einigen, wenn KE den ersten Vorschlag macht und wA den Lohn, zu dem es bei ANs Erstvorschlagsrecht kommt. In jedem Fall einigen sich beide in der ersten Periode. Dies entspringt rationalem Verhalten, denn durch Herauszögern der Einigung würde sich nur der potentielle Nutzen, den beide erlangen könnten, verringern. Diese Lösung ist lediglich eine Umformung der herkömmlichen Rubinsteinlösung und soll deshalb in Folge auch als RSL abgekürzt werden.
Inwieweit ändert sich das Ergebnis nun durch die Zulassung von Lohnangeboten über den gesamten Bereich w = [0,w°] ? Als erstes ist festzustellen, daß die gerade hergeleitete RSL auch weiterhin gilt. Die Lösung würde nicht mehr gelten, wenn sich eine der beiden Parteien durch Änderung ihrer Strategie besser stellen könnte, solange die andere ihre Strategie weiterverfolgt.
Für die AN führen alle zusätzlich möglichen Löhne w < w^ zu einem Nutzen von Null und damit weniger als bei Beibehaltung der RSL-Strategie. Sie können sich durch Änderung ihrer Strategie also nicht besser stellen.
Für die KE hingegen sind im zusätzlichen Intervall auch Nutzen größer dem, den sie in der RSL erhalten, denkbar. Allerdings da die AN w < w^ nicht akzeptieren, würde ein so lautender Vorschlag die Lohnverhandlungen in die Länge ziehen. Die Drohung der AN, solche Vorschläge nicht zu akzeptieren, ist glaubwürdig, da sie durch Verzögern sowie Scheitern der Verhandlungen niemals schlechter als durch Annahme gestellt werden. Die KE stellen sich also besser, wenn sie den AN eine positive Auszahlung anbieten, also ein Lohn w > w^, als durch kontinuierliches Zögern das Schrumpfen des möglichen Nutzens zu beobachten. Die günstigste Möglichkeit ergibt sich nach dem obigen Schema in der RSL. Die Abweichungen vom ursprünglichem Rubinsteinspiel entwerten also die Lösung nicht.
Allerdings ergibt sich nun noch eine zusätzliche Lösung. In dieser erhalten die KE den gesamten Überschuß, die AN hingegen gar nichts. Diese wird in Dow (1993) mit Residual Claimant Optimum bezeichnet und soll deshalb im weiteren mangels vernünftiger Übersetzung mit RCO abgekürzt werden.
Spielen die KE nämlich dennoch eine Strategie, die Offerten aus dem Bereich w = [0,w^] beinhaltet, gibt es eine Strategie der AN, mit der zusammen es zu einer teilspielperfekten Lösung kommt. In dieser offerieren die KE immer w* und akzeptieren lediglich Löhne w, deren Auszahlung für sie mindestens dKG* ergeben. (Hierbei bezeichnet G* das Gewinnmaximum, und w* der Lohn bei dem dieses verwirklicht wird.) In diesem Fall können die AN nie einen Vorschlag machen, den die KE akzeptieren würden und bei dem sie einen positiven Nutzen erreichen (sofern G^dKG*; siehe unten). Daher sind sie indifferent zwischen Annahme und Ablehnung des Angebotes von KE und nehmen gemäß der gemachten Annahmen das Angebot gleich an.
Tabelle 3.2: Strategien der Verhandlungslösungen im
Überblick
| KE | AN | |||
| bieten | akzeptieren | bieten | akzeptieren | |
| RSL | w = [dA(1-dK)w°
+ (1-dA)w^] /(1-dKdA) |
w [(1-dK)w°
+ dK(1-dA)w^] /(1-dKdA) |
w = [(1-dK)w°
+ dK(1-dA)w^] /(1-dKdA) |
w [dA(1-dK)w°
+(1-dA)w^]
|
| RCO | w* | alle w für die gilt: nK(w)dKG* | beliebiges | alle w |
Ist die Gewinnkurve hingegen nur schwach konkav, so daß G^ > dKG* gilt, ist es für die AN besser das Angebot von den KE abzulehnen und statt dessen bei eigenem Vorschlagsrecht in t1 diesen den Lohn vorzuschlagen, bei dem die KE dKG* als Nutzen realisieren. In diesem Fall bekämen die KE aber nur nK = d2KG*. Somit wäre ihre ursprüngliche Strategie nicht mehr optimal, denn sie hätten schon in Periode t0 durch ein anderes Angebot dKG* realisieren können, ohne durch Abdiskontierung geschädigt zu werden. Damit ist die gesamte Lösung hinfällig. Tatsächlich bleibt dann nur noch die RSL.
Ebenso würde sich für die AN eine andere Strategie auszahlen im hypothetischen Fall, daß die Gewinnfunktion nicht konstant ist, aber ihr Gewinnanteil im Intervall w = [0,w^] ansteigt. Die Nicht-Konstanz des Gewinns ist daher nicht ein ausreichender Grund für die Existenz der zweiten Lösung. Diese gilt tatsächlich nur, wenn sowohl der Nutzen für AN im gesamten Intervall w = [0,w^] gleich Null ist und die Gewinnfunktion ausreichend konkav ist. Ist dies nicht gegeben, gilt nicht mehr, daß die AN kein von KE akzeptiertes Angebot machen können, daß ihnen mehr als einen Nutzen von Null gibt.
![[Up]](../images/up.gif) 3.3 Plausibilität der Lösungen
3.3 Plausibilität der LösungenEine Strategie der AN sA ist dann dominiert von einer anderen Strategie sA´, wenn letztere bei jeder von KE gespielten Strategie zu einer Auszahlung für AN führt, die nicht kleiner ist als die von sA, aber in mindestens einem Teilspiel zu einer größeren Auszahlung führt.7
Es ist daher davon auszugehen, daß bei einem Nebeneinander von RCO und RSL es zur Einigung im Sinne der RSL kommt.
Die RSL ist allerdings nicht immer realisierbar. Abbildung 2.2 unterscheidet zwischen G^ > 0 und G^ < 0. Ist G^ < 0 kann die bevorzugte Menge x^ nicht verlustfrei produziert werden. In diesem Fall ist es unmöglich, daß beide Parteien eine positive Auszahlung erhalten, dies ist aber Voraussetzung für ihre Beteiligung an der Unternehmung. Daher fallen Lohnofferten w > w^ aus. Da die RSL aber auf solchen Lohnangeboten beruht, scheidet sie aus. In diesem Fall verbleibt das RCO, nun undominiert, als einziges Strategienpaar. Zusammengefaßt bedeutet dies, das es zur RSL kommt, wenn G^ > 0 und zum RCO, wenn G^ < 0.
![[Up]](../images/up.gif) 4 Konsequenzen der Verhandlungslösungen
4 Konsequenzen der Verhandlungslösungen![[Up]](../images/up.gif) 4.1 Verhandlungsstärke
4.1 VerhandlungsstärkeWas nun die RSL anbetrifft, ist festzustellen, daß die Verhandlungspartei mit dem höheren Diskontfaktor ( im Vorteil ist. Konkret heißt das, je größer der Diskontfaktor der einen Partei im Vergleich zu dem der gegnerischen ist, einen desto größeren Anteil vom Gewinn bekommt erstere. Im Extremfall, in dem eine Partei einen Gewinnanteil in der Folgeperiode für nichtig hält (d=0), bekommt die andere Partei den gesamten Gewinn.
Was können wir über d für AN und KE und ihrer daraus resultierenden Verhandlungsstärke als realistisch annehmen? Nehmen wir an, daß d ausdrückt, die Produktion liege still, solange verhandelt wird. Dann könnte argumentiert werden, daß die AN aufgrund geringerer finanzieller Reserven bzw. geringerer Möglichkeiten der Kreditaufnahme ein Verzögern der Verhandlungen mehr fürchten müssen als die KE und somit dA < dK sei. Andererseits müssen die KE fürchten, daß während langer Verhandlungen Wettbewerber Marktanteile erobern und somit eventuelle im voraus gemachte Investitionen sich nicht mehr rechnen.
Als weiteres Merkmal beinhaltet die RSL, daß die Partei, die den ersten Vorschlag macht, im Vorteil ist, da immer gilt wk <= wA. Bei Dow macht immer der KE den ersten Vorschlag. Dies ist eher willkürlich. Es läßt sich nicht unbedingt begründen, warum die eine oder andere Partei den ersten Vorschlag machen sollte. Am ehesten erscheint es noch so, daß der Faktor, der die Firma leitet, den ersten Vorschlag machen wird. Davon wird in dieser Arbeit daher auch ausgegangen.
![[Up]](../images/up.gif) 4.2 Symmetrie und Effizienz
4.2 Symmetrie und EffizienzAls symmetrisch gilt ein Spiel dann, wenn bei einer Verhandlung zwischen zwei gleichen Spielern, auch beide gleich hohe Auszahlungen erhalten.8
Der Einfluß des Erstvorschlagsrecht auf das Verhandlungsergebnis bringt im RS unmittelbar Asymmetrie in die Verhandlungen. Betrachten wir zunächst die RSL. So bekommt i.d.R. bei einem symmetrischen Spiel, d.h. dA = dK, der KE, einen größeren Anteil am Gesamtnutzen. Lediglich bei dA = dK -> 1, d.h., wenn Zeit für niemanden eine Rolle spielt, wird es auch zu einem symmetrischem Ergebnis kommen.
Eine Gleichverteilung der Gewinnanteile ist zwar bei vielen anderen Ausgestaltungen der Parameter möglich, allerdings beinhaltet dies immer, daß der Erstvorschläger eine geringere Discountrate hat, als der andere. Konkret ist immer dann mit einer Gleichverteilung zu rechnen, wenn für die Discountraten gilt: dK = 2 - 1/dA. Das oben diskutierte Spiel mit dA = dK = 1 ist der einzige Sonderfall, bei dem Gleichverteilung und gleiche Ausgangsbasis zusammenfallen. Diese Asymmetrie fällt weg, wenn der Abstand zwischen zwei Vorschlägen minimal wird. In diesem Fall geht wk -> wA und das Symmetrie-Axiom ist immer erfüllt.9
Beim RCO hingegen ist die Nutzenverteilung immer extrem unsymmetrisch, weil die AN unabhängig von ihrer Zeitpräferenz nie am Gewinn beteiligt werden.
Dafür bietet das RCO den Vorzug, zu einer effizienten Produktion zu führen. Da der Gewinn maximiert wird und an die KE fällt, kann keiner der beiden Parteien mehr Gewinn zugeteilt werden ohne der anderen zu schaden. Dies ist bei der RSL hingegen möglich. Das Unternehmen produziert mit x^ eine zu große Menge und schafft es nicht den maximalen Gewinn G* zu realisieren. Würden sich aber AN und KE auf die optimale Produktionsmenge x* festlegen können, könnten sie den Mehrgewinn unter sich aufteilen und beide wären besser gestellt. Dieses hingegen verbieten allerdings die Annahmen im Modell.
Es lassen sich also, von Extremfällen abgesehen, in Lohnverhandlungen nach dem Dow'schen Modell Effizienz und Symmetrie nicht vereinigen.
![[Up]](../images/up.gif) 4.3 Unternehmensorganisation
4.3 Unternehmensorganisation Betrachtet man nun das Nebeneinander von KGU und AGU im Markt,
sind zwei Ergebnisse der Lohnverhandlungen im Dow'schem Modell von besonderer
Bedeutung:
(a) Die Verhandlungslösung führt in vielen Fällen zur
Unmöglichkeit, daß der angeheuerte Faktor eine Rente erhält
(sofern es bei G^ < 0 zum RCO kommt) und
(b) dazu, daß im anderen Fall (RSL bei G^ > 0) nicht-effiziente
Produktion eintritt.
Beides hat Auswirkungen auf die Durchsetzungskraft der Unternehmensform,
(KGU bzw. AGU) im Markt.
Es setzt sich am Markt die Unternehmensform durch, die bei niedrigerem Marktpreis p noch überlebensfähig ist. Dies ist dadurch zu erklären, daß solange der Preis höher ist, neue Unternehmen noch Gewinne realisieren können und somit den Anreiz haben, in den Markt einzutreten. Bestehen kann eine Unternehmung nur, solange die Marktsituation und Organisationsform für beide Faktoren mindestens einen Nutzen von Null zuläßt. Fiele der Nutzen für einen der Faktoren ins Negative, wäre es für diesen vorteilhafter sich nicht an der Produktion zu beteiligen.
In diese Berechnung müssen nun aber neben den bisher schon berücksichtigten variablen Kosten kA(x) und kK(x), die nur bei Produktionsaufnahme anfallen, auch noch eventuelle versunkene Kosten einfließen. Letztere bezeichnen Aufwendungen, die eine Partei vor Aufnahme der Produktion hat, für spezifische Investitionen, also solchen, die an das spezielle Unternehmen gebunden sind. Der Einsatz von spezifischen Faktoren lohnt sich nur, wenn der Bereitsteller sicher sein kann, eine Rente zu erhalten, die dann die Anfangsinvestition abbezahlt. Auf KE-Seite wären solche Investitionen etwa unternehmens-spezifische Produktionsanlagen, auf AN-Seite unternehmens-spezifisches Training. Die Kosten dafür seien mit ksA, ksK bezeichnet.
Tabelle 4.1 zeigt in den oberen Zeilen die Gewinnfunktionen von AN und KE und unten die Bedingungen, die erfüllt sein müssen, um dem jeweiligen Faktor einen Anreiz zu geben, sich an der Unternehmung zu beteiligen. Aus Vereinfachungsgründen wurde hier ( als Verhandlungstärkeparameter eingeführt.10 a steigt mit der Verhandlungsstärke des Erstvorschlägers und sinkt mit der des Zweitvorschlägers.
Tabelle 4.1: Auszahlungen von KE und AN in Abhängigkeit
von Unternehmungsform und Verhandlungslösung
| KGU | AGU | |||
| RSL: G^K(p) > 0 | RCO: G^K(p) < 0 | RSL: G^A(p) > 0 | RCO: G^A(p) < 0 | |
| gK | aKG^K - ksK | G*K - ksK | (1-aA)G^A - ksK | 0 - ksK |
| gA | (1-aK) G^K - ksA | 0 - ksA | aAG^A - ksA | G*A - ksK |
| Bed. KE | G^K(p)ksK/aK | G*K ksK | G^A(p)ksK/(1-aA) | ksK = 0 |
| Bed. AN | G^K(p)ksA/(1-aK) | ksA = 0 | G^A(p)ksA/aA | G*AksA |
| Anmerkung: G, gK, gA werden als Gewinn für den gesamten Zeitraum interpretiert, für den nur einmal die spezifischen Kosten ksA, ksK anfallen. | ||||
Daraus ergibt sich, daß
(a) wenn es zum RCO kommt, die Firma nur überlebensfähig
ist, wenn der Unternehmensgewinn die versunkenen Kosten des führenden
Faktors ausgleicht und gleichzeitig der angeheuerte Faktor keine versunkenen
Kosten zu verzeichnen hat.
(b) Wenn es zur RSL kommt, ist der Bestand der Firma nur gesichert,
wenn für die KGU der Gewinn mindestens zur Kompensation von ksA/(1-aK)
bzw. ksK/aK, je nach dem,
was höher ist, ausreicht. Für die AGU gilt dies mit umgekehrten
Indizes.
Daraus läßt sich nun für verschiedene Situationen voraussagen,
welche die Gleichgewichtsunternehmung ist. Tabelle 4.2 faßt dies
zusammen.
Tabelle 4.2:11
| Fall | Verhandlungs-
lösung der |
Gleichgewichts-
unternehmung |
Gleichgewichtspreis | |
| KGU | AGU | |||
| A. G^K < 0; G^A < 0 | ||||
| 1. ksK > 0; ksA = 0 | RCO | keine | KGU | G*(p)= ksK |
| 2. ksK = 0; ksA > 0 | keine | RCO | AGU | G*(p)= ksA |
| 3. ksK > 0; ksA > 0 | keine | keine | keine | -- |
| 4. ksK = 0; ksA = 0 | RCO | RCO | beide | G*(p)= 0 |
| B. G^K > 0; G^A < 0 | ||||
| 1. ksK = 0 | RSL | RCO | AGU | G*(p) = ksA |
| 2. ksK > 0 | RSL | keine | KGU | G*(p)= max(ksK/aK; ksA/(1-aK) |
| C. G^K < 0; G^A > 0 | ||||
| 1. ksA = 0 | RCO | RSL | KGU | G*(p) = ksK |
| 2. ksA > 0 | keine | RSL | AGU | G* (p)= max(ksA/aA; ksK/(1-aA) |
| D. G^K < 0; G^A < 0 | ||||
| 1. G^K(p) < G^A(p) | RSL | RSL | KGU | G*(p) = max(ksK/aK; ksA/(1-aK) |
| 2. G^A(p) < G^K(p) | RSL | RSL | AGU | G*(p)= max(ksA/aA; ksK/(1-aA) |
Zum RCO kommt es, sofern G^ <= 0 und die versunkenen Kosten des angeheuerten Faktors null sind. Ist nur für eine der Unternehmensformen das RCO realisierbar, bildet diese die Gleichgewichtsorganisation. Die Unternehmung mit RCO verdrängt deshalb die mit RSL, weil (a) der Gewinn, der zur Deckung der versunkenen Kosten herangezogen werden kann, bei der RSL niedriger ist und (b) bei der RSL auch der andere Faktor eine Rente erhält, die die Deckung der versunkenen Kosten weiter schmälert. Ist für beide das RCO möglich, können beide Formen im Markt bestehen. (Fall A, B1, C1 in Tabelle 4.2)
Ist das RCO nicht möglich, so verbleibt, sofern nur für eine Unternehmung die RSL machbar ist, selbstverständlich diese im Markt, weil die andere gar nicht produzieren kann (Fall B2, C2).12 Ist hingegen die RSL für beide Formen realisierbar, dann setzt sich die KGU durch, sofern G^K(p) > G^A(p) wobei p den langfristigen Gleichgewichtspreis darstellt. In diesem Fall muß G^A(p) zwangsweise < 0 sein. Die AGU setzt sich entsprechend durch, wenn G^A(p) > G^K(p), G^K(p)und ist kleiner Null. In anderen Worten, es besteht die Unternehmung, die ihr gewähltes x^ zu einem niedrigerem Preis noch verlustfrei produzieren kann. (Fall D)
Aus diesen Überlegungen ergibt sich, daß den versunkenen Kosten eine wichtige Rolle in der Entscheidung über die Organisationsform der Gleichgewichtsunternehmung zukommt. In allen Fällen außer D sorgt der Markt dafür, daß diejenigen Unternehmungen bestehen, bei denen der Faktor, der versunkene Kosten zu verzeichnen hat, die Führung übernimmt. In Fall D ist das Ergebnis nicht eindeutig. Haben beide Faktoren versunkene Kosten, ist eine Produktion unter dem RCO nicht möglich, weil der angeheuerte Faktor sich keine Vergütung für die versunkenen Kosten in Form von Renten sichern kann. Dies resultiert aus der Tatsache, daß die Parteien die Produktionsmenge nicht vertraglich festlegen können und auch Ausgleichszahlungen neben dem Lohn nicht möglich sind. Ansonsten gäbe es die Möglichkeit, den an und für sich ausreichenden Gewinn G*, den versunkenen Kosten entsprechend aufzuteilen. Dies impliziert auch, daß wenn beide Faktoren unternehmens-spezifische Investitionen tätigen müssen, effiziente Produktion ausgeschlossen ist.
![[Up]](../images/up.gif) 5 Schlußbemerkungen
5 SchlußbemerkungenAllerdings findet die Aussagekraft auch dieses Modells seine Grenzen in der Beschränkung durch die gemachten Annahmen. So ist zu vermuten, daß Lohnverhandlungen tatsächlich in anderer als hier angenommener Form ablaufen. Das Modell bietet z.B. keine Erklärung für Streiks, da in den Verhandlungslösungen immer eine sofortige Einigung eintritt. Ein Manko mag diesbezüglich die sehr unwahrscheinliche Voraussetzung von vollkommener Information auf beiden Seiten sein.13
![[Up]](../images/up.gif) Anhang
Anhang![[Up]](../images/up.gif) Herleitung von wk und wA
Herleitung von wk und wA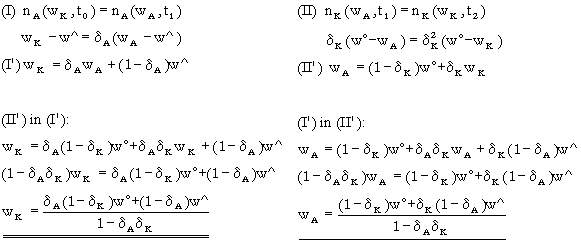
![[Up]](../images/up.gif) Abkürzungsverzeichnis
AbkürzungsverzeichnisAN Arbeitnehmer
KE Kapitaleigner
KGU Kapitaleigner-geführte Unternehmung
RCO Residual Claimant Optimum
RS Rubinsteinspiel
RSL Rubinsteinlösung
![[Up]](../images/up.gif) Symbolverzeichnis
Symbolverzeichnis| sA, sK | Strategien von AN bzw. KE |
| aA, aK | Verhandlungsstärkeparameter bei AGU und KGU |
| dA, dK | Discountraten von AN bzw. KE |
| E | Erlös |
| G | Gewinn, Überschuß der Unternehmung |
| G^ | Gewinn bei Produktion von x^ |
| G* | Maximalgewinn |
| gA, gK | Gewinnanteile von AN bzw. KE |
| K | Gesamtkosten der Unternehmung |
| kA, kK | Kosten von AN bzw. KE durch Beteiligung an der Produktion |
| ksA, ksK | Versunkene Kosten von AN bzw. KE |
| nK, nA | Nutzen für KE bzw. AN |
| p | Preis |
| p | Preis im langfristigen Gleichgewicht |
| t | Verhandlungsperiode |
| w | Lohn |
| w° | Höchstmöglicher Lohn ohne Verlust |
| w^ | Niedrigster Lohn, um x^ herzustellen |
| w* | Gewinnmaximaler Lohn |
| wK, wA | Lohn, wenn KE bzw. AN ersten Vorschlag machen |
| x | Produktionsmenge |
| x^ | Produktionsmenge, die Gewinnanteil des unternehmens-führenden Faktors maximiert |
| x* | Gewinnmaximierende Produktionsmenge |
![[Up]](../images/up.gif) Literaturverzeichnis
LiteraturverzeichnisDow, G.K. (1993): Why Capital Hires Labor, in: American Economic Review, Band 83, S. 118-134.
Friedman, J.W. (1991): Game Theory with Applications to Economics, 2. Auflage, Oxford University Press, New York - Oxford.
Holler, M.J. Und Illing, G. (1993): Einführung in die Spieltheorie, 2. Auflage, Springer Verlag, Berlin usw.
Osborne, M.J. und Rubinstein, A. (1990): Bargaining and Markets, Academic Press, San Diego usw.
Rubinstein, A. (1982): Perfect Equilibrium in a Bargaining
Model, in: Econometrica, Band 50, S. 97-111.